1. Directions

For questions 1 through 15, solve each problem, choose the best answer from the choices provided, and fill in the corresponding circle on your answer sheet. For questions 16 through 20, solve the problem and enter your answer in the grid on the answer sheet. Please refer to the directions before question 16 on how to enter your answers in the grid. You may use scratch paper for scratch work.

Notes

1. The use of a calculator is not permitted.

2. All variables and expressions used represent real numbers unless otherwise indicated.

3. Figures provided in this test are drawn to scale unless otherwise indicated.

4. All figures lie in a plane unless otherwise indicated.

5. Unless otherwise indicated, the domain of a given function f is the set of all real numbers x for which (x) is a real number.

Reference

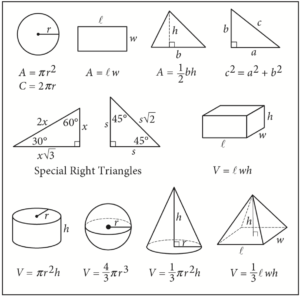
Begin skippable figure descriptions.

The figure presents information for your reference in solving some of the problems.

Reference figure 1 is a circle with radius r. Two equations are presented below reference figure 1.

A equals pi times the square of r.

C equals 2 pi r.

Reference figure 2 is a rectangle with length ℓ and width w. An equation is presented below reference figure 2.

A equals ℓ w.

Reference figure 3 is a triangle with base b and height h. An equation is presented below reference figure 3.

A equals onehalf b h.

Reference figure 4 is a right triangle. The two sides that form the right angle are labeled a and b, and the side opposite the right angle is labeled c. An equation is presented below reference figure 4.

c squared equals a squared plus b squared.

Special Right Triangles

Reference figure 5 is a right triangle with a 30degree angle and a 60degree angle. The side opposite the 30degree angle is labeled x. The side opposite the 60degree angle is labeled x times the square root of 3. The side opposite the right angle is labeled 2 x.

Reference figure 6 is a right triangle with two 45degree angles. Two sides are each labeled s. The side opposite the right angle is labeled s times the square root of 2.

Reference figure 7 is a rectangular solid whose base has length ℓ and width w and whose height is h. An equation is presented below reference figure 7.

V equals ℓ w h.

Reference figure 8 is a right circular cylinder whose base has radius r and whose height is h. An equation is presented below reference figure 8.

V equals pi times the square of r times h.

Reference figure 9 is a sphere with radius r. An equation is presented below reference figure 9.

V equals fourthirds pi times the cube of r.

Reference figure 10 is a cone whose base has radius r and whose height is h. An equation is presented below reference figure 10.

V equals onethird times pi times the square of r times h.

Reference figure 11 is an asymmetrical pyramid whose base has length ℓ and width w and whose height is h. An equation is presented below reference figure 11.

V equals onethird ℓ w h.

End skippable figure descriptions.

Additional Reference Information

The number of degrees of arc in a circle is 360.

The number of radians of arc in a circle is 2 pi.

The sum of the measures in degrees of the angles of a triangle is 180.

Question 1.

A painter will paint n walls with the same size and shape in a building using a specific brand of paint. The painter’s fee can be calculated by the expression nKℓh where n is the number of walls, K is a constant with units of dollars per square foot, ℓ is the length of each wall in feet, and h is the height of each wall in feet. If the customer asks the painter to use a more expensive brand of paint, which of the factors in the expression would change?

2. If   3r = 18, what is the value of 6r + 3?

3. Which of the following is equal to , for all values of a?

4. The number of states that joined the United States between 1776 and 1849 is twice the number of states that joined between 1850 and 1900. If 30 states joined the United States between 1776 and 1849 and x states joined between 1850 and 1900, which of the following equations is true?

5. If  , what is the value of ?

6. Question 6 refers to the following equations.

 2x – 3y = -14

 3x – 2y = -6

Question 6.

If (x,y) is a solution to the preceding system of equations, what is the value of x – y?

7. Question 7 refers to the following table.

Question 7.

The function f is defined by a polynomial. Some values of x and  f(x) are shown in the preceding table. Which of the following must be a factor of  f (x)?

8. The liney = kx + 4, where k is a constant, is graphed in the xyplane. If the line contains the point (c,d), where   and  what is the slope of the line in terms of c and d?

9. Question 9 refers to the following system of equations.

kx – 3y = 4 

 4x – 5y = 7

Question 9.

In the preceding system of equations, k is a constant and x and y are variables. For what value of k will the system of equations have no solution?

10. In the xyplane, the parabola with equation , intersects the line with equation y = 25 at two points, A and B. What is the length of ?

11. Question 11 refers to the following figure.

Begin skippable figure description.

The figure presents three lines k, l, and m that intersect at a point. The three lines form six angles at the point of intersection. The horizontal line is labeled m, the line that slants upward and to the right is labeled l, and the line that slants downward and to the right is labeled k. Of the 6 angles, 3 angles are above line m, and 3 angles are below line m. Starting from the leftmost angle above line m and going clockwise, the 6 angles are labeled x degrees, y degrees, z degrees, t degrees, u degrees, and w degrees, respectively.

End skippable figure description.

Question 11.

In the preceding figure, lines k, ℓ, and m intersect at a point. If x + y = u + w, which of the following must be true?

I.   x = z

II.   y = w

III.   z = t

12. Question 12 refers to the following quadratic equation.

y = a(x – 2)(x +4)

Question 12.

In the preceding quadratic equation, a is a nonzero constant. The graph of the equation in the xyplane is a parabola with vertex(c,d). Which of the following is equal to d?

13. The equation   is true for all values of  where a is a constant. What is the value of a ?

14. What are the solutions to ?

15. Question 15 refers to the following equation.

Question 15.

The preceding equation shows how a temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?

I. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of    degree Celsius.

II. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.

III. A temperature increase of    degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.

16. Directions

For questions 16 through 20, solve the problem and enter your answer in the grid, as described below, on the answer sheet.

1. Although not required, it is suggested that you write your answer in the boxes at the top of the columns to help you fill in the circles accurately. You will receive credit only if the circles are filled in correctly.

2. Mark no more than one circle in any column.

3. No question has a negative answer.

4. Some problems may have more than one correct answer. In such cases, grid only one answer.

5. Mixed numbers such as   must be gridded as 3.5 or 7/2. (If , is entered into the grid, it will be interpreted as   , not .)

6. Decimal answers: If you obtain a decimal answer with more digits than the grid can accommodate, it may be either rounded or truncated, but it must fill the entire grid.

The following are four examples of how to record your answer in the spaces provided. Keep in mind that there are four spaces provided to record each answer.

Examples 1 and 2

Begin skippable figure description.

Example 1: If your answer is a fraction such as seventwelfths, it should be recorded as follows. Enter 7 in the first space, the fraction bar (a slash) in the second space, 1 in the third space, and 2 in the fourth space. All four spaces would be used in this example.

Example 2: If your answer is a decimal value such as 2.5, it could be recorded as follows. Enter 2 in the second space, the decimal point in the third space, and 5 in the fourth space. Only three spaces would be used in this example.

End skippable figure description.

Example 3

Begin skippable figure description.

Example 3: Acceptable ways to record twothirds are: 2 slash 3, .666, and .667.

End skippable figure description.

Example 4

Note: You may start your answers in any column, space permitting. Columns you don’t need to use should be left blank.

Begin skippable figure description.

Example 4: It is not necessary to begin recording answers in the first space unless all four spaces are needed. For example, if your answer is 201, you may record 2 in the second space, 0 in the third space, and 1 in the fourth space. Alternatively, you may record 2 in the first space, 0 in the second space, and 1 in the third space. Spaces not needed should be left blank.

End skippable figure description.

Question 16 refers to the following equation.

Question 16.

If x > 0, what is one possible solution to the preceding equation?

17. If  , what is the value of x?

18. Question 18 refers to the following figure.

Begin skippable figure description.

The figure presents two triangles that have one vertex in common. The two triangles, one on the left and one on the right, each have a vertical side opposite the common vertex, and the other two sides in each triangle are marked showing that both sides are equal in length. In the triangle on the left, the angle at the common vertex is labeled y degrees, and in the triangle on the right, the angle at the common vertex is labeled z degrees. The exterior angle of the triangle on the right that is between one of the equal sides and the vertical line extended from the vertical side is labeled x degrees.

End skippable figure description.

Question 18.

Two isosceles triangles are shown in the preceding figure. If 180 – z = 2y and   y = 75, what is the value of x?

19. At a lunch stand, each hamburger has 50 more calories than each order of fries. If 2 hamburgers and 3 orders of fries have a total of 1700 calories, how many calories does a hamburger have?

20. In triangle ABC, the measure of  is 90°, BC  = 16, and AC = 20. Triangle DEF is similar to triangle ABC, where vertices D, E, and F correspond to vertices A, B, and C, respectively, and each side of triangle DEF is   the length of the corresponding side of triangle ABC. What is the value of sinF?